Семь раз отмерь, один отрежь.
Русская
пословица.
Игра Точки представляет собой европейскую версию древней японской игры Го. Не одно поколение студентов усердно практикуются в ней во время долгих и утомительных лекций. Бумага в клетку и две ручки разного цвета - все что нужно, чтобы отвлечься от монотонного голоса лектора и погрузится в увлекательный мир стен, блокад, осад, окружений и пленных.
Эта статья посвящена математическим методам и программным алгоритмам, реализующим поиск оптимальных ходов в точках. О сложности этой задачи известно давно. Причин тому несколько, одна из которых - огромное число всевозможных позиций в точках. Для сравнения: в шахматах общее число возможных партий составляет около 1040 , в игре Го это число возрастает до 10120, а в точках число всевозможных позиций на поле 30x30 составляет 10270. В начале партии в шахматах можно сделать около 20-ти различных ходов, в точках - 900. Соответственно дерево просчета ходов в шахматах разрастается как геометрическая прогрессия с основанием 20 , а в точках - с основанием 900. Но главное не это. Основная сложность точек заключается не в огромном числе всевозможных позиций, а в том, что точки это игра в основном позиционная, в отличие от тех же шахмат, которые являются в большей степени логической игрой. Смысл точек состоит в окружении как можно большего числа точек противника. При этом стена окружения может состоять из многих десятков точек. Человеческий мозг, как устройство параллельной обработки информации, без труда может охватить такое множество точек. Глаз человека мгновенно обнаруживает замкнутость области (или почти мгновенно - около одной десятой доли секунды). Другое дело - компьютер. Одна только задача обнаружения замкнутости области на игровой доске - нетривиальная задача, решение котрой требует сложных рекурсивных алгоритмов. Еще сложнее для него - определить какие же именно точки попадают в окружение. А ведь такой анализ нужно проводить после каждого реального или просчитываемого хода... Если к этому еще и прибавить огромное дерево вариантов развития партии, то становится понятно, почему в мире существуют тысячи отличных программ, играющих в шахматы, но ни одной стоящей программы, более-менее хорошо играющей в точки или Го.
Однако оставим пространные рассуждения и приступим к конкретике. Я на протяжении нескольких лет время от времени возвращался к этой задаче, но до конкретных алгоритмов дело не доходило. И вот летом, во время отпуска, я сел за машину и решил написать программку, которая более или менее достойно играла бы в точки. Не буду останавливаться на тех идеях, которые я реализовывал, но которые не давали должного эффекта. Хочу лишь описать те методы, которые дали ощутимый результат и могут найти достаточно хорошее решение задачи за разумное время. Не буду останавливаться на алгоритмах обнаружения замкнутых областей, моделирования дерева вариантов и на их конкретной программной реализации. Это по плечу каждому хорошему программисту. Хочу остановиться только на ключевых моментах отбора ходов и оценки позиции.
В данной статье я не привожу достаточно серьезных и строгих математических доказательств применяемых методов. Да это наверно и не нужно. Эффективность методов доказывает уровень игры программы :)
Для оценки позиции я беру в первую очередь разность между числом окруженных точек противника и своими окруженными точками. Это единственный точный критерий, по которому можно определить реальное положение дел на доске. Но хотя этот критерий и является основным, он далеко не всегда позволяет найти оптимальный ход, поскольку число окруженных точек в партии меняется достаточно редко, и уж очевидно, не после каждого хода. Поэтому я ввел понятие важности точки, величина которой определяется исходя из некоторых эвристических правил. Выбор оптимального хода основывается на числе окруженных точек, но если при просчете в глубину дерева этот критерий не меняется, то выбор хода основывается на поиске точки с максимальной важностью.
Отмечу важную деталь: я разделяю понятия оценки позиции и оценки хода(для избежания путаницы назову ее оценкой важности хода). Оценку важности возможных ходов я делаю только один раз - для текущей позиции на доске. При поиске же в глубину дерева ходов я опираюсь только на оценку позиции. Если минимакс этой оценки при данной глубине поиска не зависит от выбора текущего хода (то есть от выбора вершины первого яруса дерева вариантов), то выбор делается только на основе оценки хода (важности точки), в противном случае - по интегральной оценке, сочетающей важность хода и просчитанную вглубь оценку результирующей позиции, с доминирующим коэффициентом для второго слагаемого. Проще говоря, оценка хода (не в смысле важности, а в смысле инегральной оценки) для клетки с координатами (x,y) имеет вид:
F(x,y)=k1*Importance(x,y)+k2*MinMax(kill2m-kill1m) (1)
где 0< k1<< k2 - некоторые коэффициенты, m-глубина просчета, kill2 и kill1 - число окруженных точек противника и число своих окруженных точек соответственно. MinMax рассчитывается на множестве вершин дерева вариантов и представляет собой функцию минимакса (не буду ее расписывать, ее вид хорошо известен из теории игр). Заметим, что важность точки Importance(x,y) рассчитывается только для свободных клеток, не зависит от глубины просчета m и от стороны, для которой она рассчитывается. То есть важность пустой клетки имеет одинаковую величину как для синих, так и для красных. Помимо этого, важность может быть как положительной, так и отрицательной. Отметим еще два момента: важность любой точки может поменяться после очередного хода как в большую, так и в меньшую сторону (т.е. это величина немонотонная); функция минимакса также немонотонна при движении вглубь дерева вариантов. Это очевидно, так как на каждом ходу существует вероятность захвата любой из сторон произвольного числа точек оппонента.

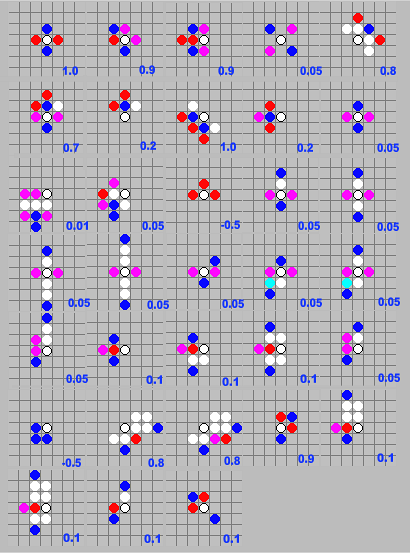
Выбор эвристик был сделан на основе моего личного опыта и, конечно, не является безаппиляционным. Тем не менее он показывает неплохие результаты (хотя, опять же, это очень специфично и зависит от стиля игры противника). На рисунке представлены 33 эвристики. Перед началом поиска оптимального хода программа просматривает все точки игрового диапазона (см. ниже) и для каждой свободной точки пытается применить каждое из 33 правил. При этом на рисунке представлены позиции с точностью до симметрии. Каждая эвристика на самом деле предстваляет группу из 16 симметричных позиций: четыре симметрии поворота, еще четыре для зеркальных позиций, и все это рассматривается для прямой и инверсной ситуаций (когда синие точки заменяются на красные, розовые на голубые и т.д.). Таким образом, если в игровом диапазоне находится 30 свободных точек, то необходимо унифицировать около 33*16*30=15840 позиций, каждая из которых, в среднем, состоит из 5 точек. Несмотря на внушительность цифры, применяя элементарные оптимизационные приемы, рассчет важности выполняется очень быстро и занимает копеечное время по сравнению с просчетом дерева вариантов (ведь эта операция делается только единожды, перед поиском оптимального хода).
Величина важности для позиций определялась интуитивно и на основе тестовых партий. Но я придерживался некоторых правил. Так, например, если в позиции участвуют как синие, так и красные точки, то важность не опускается ниже 0.1 (по модулю), если же в позиции участвуют точки только одного цвета плюс полуцветов (розовые или голубые), то оценку не желательно устанавливать выше 0.05 (по модулю).
Если точка удовлетворяет нескольким эвристикам одновременно, то в качестве важности выбирается величина максимальной оценки (но не сумма оценок!).
В принципе, набор стандартных позиций программа может генерировать и сама, в процессе обучения у противника. Но здесь возникает ряд трудностей к преодолению которых я не приблизился ни на йоту. Если противник на каком-то этапе игры сумел выиграть точки, значит он сделал какие-то ходы которые привели его к успеху, и программе было бы неплохо запомнить эту ситуацию. Но как определить какой именно ход привел к успеху? Маловероятно, что это был последний ход, который собственно окружил точки. Конечно программа при просчете вперед начинает "чувствовать" неизбежность окружения за несколько ходов до собственно окружения, и, понятно, что ключевой ход был сделан до момента обнаружения этого. Но как давно до этого был сделан этот ход? Кроме этого, как определить какие именно точки позиции имели влияние на окружение, а какие нет? Это, правда, можно определить с помощью алгоритмов абстракции при многократном повторении аналогичных позиций. Но вероятность повтора позиции довольно низка и эффективность этого метода, наверное, окажется тоже очень низкой. Есть еще один метод — метод самообучения — когда программа делает глубокий просчет вперед, находит оптимальный ход и запоминает его в виде эвристики (если этот ход ведет к неизбежной потере точек противником). Тогда, в будущем, она сможет применять результаты глубокого просчета, не делая собственно сам просчет. Конечно, далеко не всякая позиция может быть применимой в большом числе ситуаций. Многие позициии являются очень специфичными и содержать очень большое число значимых точек-участников. Такие позиции не имеет смысла использовать как эвристику, поскольку вероятность применимости позиции в игре очень низка. Однако, если такие стандартные позиции (с достаточно малым числом точек) все же существуют, то этот метод их найдет (беда в том, что для этого ему, возможно, придется просчитывать на очень большую глубину, настолько большую, что это будет невозможно).(не очень сумбурно написано ??).
Помимо приведенных выше эвристик, я также применял эвристики другого типа, которые присваивали положительную важность угловым точкам (тем точкам, у которых в прямой видимости, под прямым углом, находятся точки одного цвета, и расстояние до них больше единицы). Аналогичные частные случаи представлены в эвристиках № 5,27,28 на рисунке.
Теперь приступим к рассмотрению самого интересного — дерева вариантов. Как уже отмечалось, оценка позиции немонотонно меняется при движении вглубь дерева вариантов. Немонотонность и малопредсказуемость оценки делает невозможным применение метода ветвей и границ (альфа-бета процедуры), поскольку нет непосредственных критериев, позволяющих оценить снизу или сверху величину оценочной функции при движении по некоторой ветви дерева. Но, как оказалось, есть достаточно эффективные методы отсечения ветвей дерева. В принципе, описанный ниже метод основывается на относительной статичности позиции в точках. Объясню более подробно, что я хочу этим сказать: сама по себе позиция в точках мало меняется с новыми ходами, поскольку те точки, которые уже есть на доске не двигаются и не исчезают. Поэтому, если мы, например, хотим просчитывать дерево на 3 полных хода вперед, то позиция (в смысле расположения точек) существенно измениться не может, ведь противник успеет за это время поставить лишь три точки, что достаточно мало по сравнению с числом точек которые уже стоят на доске (речь идет о середине партии, а не о самом ее начале). Учитывая свойство позиции оставаться относительно неизменной, мы можем задуматься: а не имеет ли смысл просчитать свои ходы вперед, и при этом как бы "забыв" о ходах противника? Сделав такой просчет, мы можем получить почти наилучшее (для себя) значение оценочной функции, которое может только ухудшится если бы противник действительно ходил бы. Максимум на сколько мы можем ошибаться, это как раз на те три точки, которые противник не ставил, но которые мы как бы теоретически могли бы окружить (а точнее даже не три, а две, поскольку мы ходим первые). На самом деле, вероятность того, что противник поставит эти точки как раз внутрь области, которую мы тут же окружим, черезвычайно низка, и мы можем этой возможностью пренебречь. Таким образом, если мы собираемся просчитывть дерево вариантов на m полных ходов вперед, то мы можем оценить свой выигрыш сверху (без учета важности точек, про которую мы пока забудем), моделируя только свои хода, и не учитывая ответные ходы противника:
Fmax=k2*max(kill2m-kill1) (2)
где kill1 - число взятых наших точек на данный момент, kill2m - число взятых точек противника, если бы мы поставили еще m точек, а противник бы не сделал бы ни одного хода. Понятно, что если бы противник все же делал бы ответные ходы, то результирующая оценка (1) не могла бы превышать значения (2), за исключением практически невероятных случаев, когда противник играет в "поддавки". Но и в таком случае, мы можем точно опредилить максимум оценочной функции:
F'max=k2*max(m-1+kill2m-kill1) (2')
Но, на практике, я все же пользовался оценкой (2). Оценка (2') является завышенной (хотя и более точной) и, при предположении об оптимальности действий противника, фактическое ее достижение почти невозможно (разве что в самом конце партии, когда противник будет ходить вынужденно, из-за отсутствия свободных клеток).
Таким образом, смоделировав только свои ходы, мы получили оценку сверху целевой функции. Аналогично, моделируя только ходы противника, мы получим оценку снизу:
Fmin=k2*min(kill2-kill1m) (3)
Итак, получен диапазон значений целевой функции, и мы можем воспользоваться им для применения метода ветвей и границ следующим образом: если при просмотре дерева вариантов мы достигли значения целевой функции равного Fmax(или почти равного - с точностью до коэффициента k1), то дальнейшего просмотра дерева можно не делать, поскольку более высокого значения функции мы все равно не достигнем, а найденный ход можно считать оптимальным. Далее, если Fmin= Fmax , то это означает, что взятия невозможны (для глубины просчета m), и для оценки хода можно пользоваться только первым слагаемым из (1) и просчета вперед вообще не делать, поскольку второе слагаемое из (1) всегда будет равно нулю.
Однако, не будем забывать, что для получения граничных оценок требуется делать дополнительный поиск в дереве, и этот поиск занимает определенное время. Оценим это время. Исходя из того, что на каждом ходу в рамках игрового диапазона возможно сделать около 30 различных ходов, то для предварительного рассчета минимума целевой функции требуется просмотреть порядка 30m позиций, и столько же для нахождения максимума. Всего, при глубине m=3, число рассматриваемых позиций равно 2*303=54000. Для просмотра же основного дерева вариантов (моделирование своих ходов и ходов противника) требуется просмотр 302m позиций, что при m=3 составляет 729000000. Таким образом, время на предварительные рассчеты составляет лишь 0.007% от времени полного просчета, что безусловно делает применение предварительного поиска очень эффективным методом обрезания дерева, поскольку ничтожное время потраченное на предварительный просчет может сэкономить очень много времени при исследовании основного дерева. Причем, чем более глубокий просчет мы делаем, тем более эффективным становится использование этого метода.
Основная проблема при поиске в дереве — его размер, который зависит в первую очередь от числа проверяемых вариантов на каждом полуходу. Отсечение бесполезных вариантов — самый верный способ сокращения размера дерева. Бесполезными ходами можно считать те хода, при которых моделирование на глубину n не приводит к изменению целевой функции. Проще говоря, если поставленные точки ничего не окружают. И наоборот, полезные ходы участвуют в некоторых траекториях, которые приводят к окружению точек противника (опять же заметим, что речь идет о просчете на ограниченную глубину). Потенциально же, конечно, любая точка в отдаленном будущем может участвовать в окружающей траектории. Но, поскольку мы просматриваем только на глубину n, то о более дальних перспективах мы все равно ничего сказать не можем (для нас они просто не существуют). Итак, назовем окружающей траекторией множество незанятых точек, при заполнении которых одним цветом происходит окружение точек противника. Далее выведем логическое следствие: если глубина просчета n, то точки, не участвующие ни в одной окружающей траектории(независимо своей или противника) длинны не более n, являются бесполезными. Поясним этот не совсем тривиальный вывод. Рассмотрим три случая, которые могут влиять на целевую функцию:
1. Атака: Мы окружаем точки противника. Очевидно, что в таком случае не имеет смысла ставить точки вне своих окружающих траекторий, поскольку, по определению, такие точки не могут участвовать в окружении.
2. Пассивная защита: Противник пытается нас окружить, и мы ему препятствуем, занимая пустые точки его окружающих траекторий. В таком случае мы должны занимать точки, лежащие на окружающих траекториях противника, и не имеет смысла ставить точки в другие поля, так как эти ходы не помешают противнику заполнить траекторию.
3. Активная защита: Противник пытается нас окружить, а мы ему препятствуем посредством окружения части его окружающей стены (разрыв стены). Поскольку речь идет о окружении части стены противника, то такой случай на самом деле относится к атаке, и следовательно, такие точки также относятся к нашим окружающим траекториям.
Таким образом, если пустая точка не принадлежит ни к одной из траекторий (своей или противника), то такая точка бесполезна как для нас, так и для противника, и ходы в эту точку можно не моделировать. Такое отсечение бесполезных ходов дает огромное сокращение дерева вариантов. Число возможных полуходов внутри игрового диапазона может сокращается в 3-10 раз(при глубине просчета 3 полных хода). Пусть мы отсекаем только две трети точек. Даже в таком случае число позиций сокращается с 306 до 106, то есть в 729 (!) раз (для стандартной позиции с 30-ю возможными ходами в игровом диапазоне и глубине просчета в 3 полных хода). Во столько же сокращается и время просчета. Фактически применение этого метода отсечения позволяет увеличить глубину просчета на один полный ход, поскольку 729~302 . Следует отметить, что эффективность этого метода не возрастает с увеличением глубины просчета, поскольку число окружающих траекторий растет экспоненциально с увеличением их длинны, а следовательно и глубины просчета. Таким образом, при больших глубинах просчета может оказаться так, что все точки игрового диапазона находятся на окружающих траекториях, и эффективоность метода упадет до нуля. Однако, на практике, глубина просчета никогда не будет превышать 5-6 полных хода, поэтому метод всегда будет эффективен.
Для нахождения окружающих траекторий я использовал моделирование ходов только одной из сторон при нахождении верхних и нижних оценок целевой функции (см. предыдущую главу). Если некторая комбинация выставленных точек приводила к окружению, точки вносились в список окружающих траекторий. Формировалась двумерная таблица, строки которой соответствовали точкам, а столбцы - траекториям. Если точка относилась к окружающей траектории, в соответствующей ячейке таблицы ставилась 1. Таким образом, нахождение траекторий проводилось одновременно с предварительным поиском оценок и почти не занимало дополнительных расходов времени.
Использование моделирования ходов только одной из сторон позволяет найти окружающие траектории, но не все. Причина в том, что в реальной игре точки ставятся игроками попеременно, и при выставлении новых точек противником могут возникать новые траектории, окружающие эти новые точки. Однако, как уже отмечалось ранее, эта неполнота просчета мало влияет на результативность игры. Тем более, что после реального хода противника, траектории будут пересчитаны заново, и, таким образом, в реальной игре просчитанные траектории всегда будут оставаться актуальными. Погрешность же касается лишь моделирования при просчете вперед и начинает незначительно сказываться при увеличенни глубины просчета (начиная с глубины в 2 полухода). Конечно, при больших глубинах мы бы уже не смогли пренебрегать окружением вновь поставленных точек, однако, при реальных глубинах (3-4 хода) мы рискуем максимум 3-мя точками, и то при очень малой вероятности достичь их фактического окружения.
Метод моделирования только полезных ходов, описанный в предыдущей главе, — основной метод сокращения времени просчета. Он дает сокращение времени на несколько порядков. Но информация, полученная о тракториях, может быть использована и в дальнейшем, в самом процессе моделирования. Здесь существует несколько эвристик, позволяющих отбросить некоторые траектории и соответственно уменьшить дерево вариантов. Первоначально я придумал достаточно мощный метод отсечения траекторий. Но в последствии со многими идеями пришлось расстаться. Они оказались либо очень сложными в реализации, либо я находил специфические случаи, котрые было невозможно учесть в этих методах. Некторые идеи я опишу в заключении, а сейчас остановлюсь на двух эвристиках, которые были реализованы на практике.
1. Пусть на некотором этапе моделирования нам осталось поставить n точек, а для замыкания некоторой траектории требуется большее число точек, чем n, то такую траекторию можно отбросить, поскольку мы не сможем ее заполнить до конца. То же самое касается траекторий противника. (Отмечу, что отбрасывание траекторий еще не означает сокращения дерева вариантов, ведь точка исключатся из числа моделируемых ходов, только если она не входит ни в одну траекторию. А на практике лишь малая часть точек принадлежит только одной траектории.). Эта эвристика применяется каждый раз при выборе хода (т.е. она применяется столько раз, сколько листьев в дереве вариантов).
2. Траектория, которая не пересекается ни с одной траекторией противника и содержит более 1-й точки, принадлежащей только ей, исключается из списка траекторий. Эта эвристика применяется один раз, перед поиском в дереве.
Причина исключения такой траектории в том, что противник в любой момент может пресечь эту траекторию, заняв одну из точек, принадлежащих только этой траектории.
Трудно доказать то, что последняя эвристика не отсекает полезных точек, но ее эффективность была проверена на нескольких тестовых примерах. Во всех случаях оптимальный ход был найден.
Рассмотрим эффективность эвристик на конкретном примере:
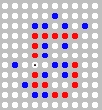
Задача показанная на рисунке имеет одно единственное решение (ход синих), показанное черной точкой. Это решение может быть найдено при глубине просчета не менее чем 3 полных хода. В таблице показано время и число рассмотренных вершин дерева вариантов с применением эвристик и без:
|
Глубина просчета n, полных ходов |
Метод отсечения |
Число моделируемых вершин дерева |
Время просчета*, мин:сек |
Правильность решения задачи |
|
3 |
Просмотр всех ходов в игровом диапазоне |
216 360 144 000 |
~1700 часов |
Да |
|
3 |
Просмотр всех полезных ходов |
9 532 753 |
4:30 |
Да |
|
3 |
Просмотр полезных ходов с применением 1-й эвристики |
102 475 |
0:20 |
Да |
|
3 |
Просмотр полезных ходов с применением 1-й и 2-й эвристик |
65 409 |
0:11 |
Да |
К сожалению, даже при применении эвристик, время просчета позиции на глубине трех ходов может составлять несколько минут (а в худших случаях и несколько десятков минут). В игровом варианте программы пришлось поставить ограничение на время просчета с той целью, чтобы игра не теряла динамизма. Таким образом, происходил неполный перебор вариантов. В связи с этим имеет смысл использовать еще одну эвристику:
Ходы рассматриваются в порядке убывания числа вхождения данной точки в различные траектории (это не касается самой первой рассматриваемой точки, которая, как уже отмечалось, определяется по максимуму важности). Эта эвристика применяется только для первого яруса дерева вариантов.
При полном просмотре дерева порядок просмотра не имеет значения. Но если происходит грубое отсечение непросмотренных ветвей дерева, то такая эвристика повышает вероятность нахождения оптимального хода.
Вот собственно и все, что удалось реализовать. Рассмотренные методы позволяют программе вести игру в разумных временных диапазонах на глубине 3 полных хода. При глубине 3.5 и 4 хода время просчета уже становится неприемлемым. И без кардинально новых эвристик существенно сократить время просчета наврядли удастся.
Среди кардинальных решений могу предложить следующую идею: разделять множество полезных ходов на несколько непересекающихся частей и вести поиск только внутри этих подмножеств. Такое разделение позволит сократить суммарное число вершин дерева на несколько порядков. На практике человек именно таким образом и действует: он не просчитывает ходы на всем поле. Он просчитывает действия на конкретном, локальном учатске поля. Единственный вопрос — как именно разделить множества точек? Первое, что приходит в голову — разделить множества траекторий на непересекающиеся классы (кстати, эти классы можно найти, умножив матрицу точек-траекторий на саму себя транспонированную), и моделировать только внутри этих классов. Но, к сожалению, так просто эту задачу не решить. Причина в том, что траектории представляют только часть окружающих стен. И даже если траектории не пересекаются, они на самом деле могут быть связаны общими окружающими стенами. Например, одна заполненная траектория может блокировать другую траекторию, просто потому что она попадет внутрь окружающих стен.
Несмотря на сложности, задача разделения дерева на подклассы все же решаема при условии, что найдется алгоритм учета взаимодействий различных траекторий и их классов. Тогда просчет дерева на 4-5 ходов станет реальностью.
Помимо увеличения глубины просчета, имеет смысл совершенствовать методы нахождения стратегии игры. Приведеные алгоритмы хорошо играют только в тактике, на малых, ограниченных участках. Почти полное отсутствие стратегии игры (кроме некоторых эвристик при подсчете важности) ведет к неминуемому проигрышу человеку. Моделирование стратегии возможно занимает не так-то и много машинного времени (тем более что его не обязательно производить перед каждым ходом, достаточно делать это время от времени), но затруднительно нахождение самих алгоритмов нахождения и реализации стратегии. Пока конкретных алгоритмов или идей на этот счет у меня нет.
P.S. Работающую версию программы можно скачать здесь:))
P.P.S. Также стоит заглянуть сюда Логическая игра Точки
©tps99@mail.ru), 2002. All rights reserved.